Introduction

In India, commodity trading was banned with the apprehension that it will lead to speculation, unethical hoarding and profiteering which will push up the prices (Biswal, 2008). In May 2003, through a notification, the Government of Indi, revoked the prohibition on commodity futures trading (Biswal, 2008) and established three national-level commodity exchanges. Multi Commodity Exchange (MCX) is the leading commodity exchange which accounts for a major percentage of the total commodity trading in India. Since 2003, commodity futures trading in India has been showing significant growth both in terms of volume and value. In the financial year 2019–2020, the average daily turnover of commodity futures in India touched `34,491 crores which is more than a 23% increase from the previous year (Commodity Insight Year Book 2019–2020, MCX).

Manifold’s increase in the market turnover of commodity futures attracts the researchers for in-depth analysis. The information content of the data has become the main point of attraction for researchers, policymakers and investors. Change in demand and supply position affects the price and with the change in price different traders reacts differently having different information content. Participation of different investors with diverse national and global information brings price equilibrium to the market. The trading volume contains important information which is very useful for different market participants Srinivasan et al. (2016).

According to Biswas and Rajib (2011), ‘a change in demand induces a price change and subsequently adjustment takes place in price and trading volume until a new equilibrium is arrived at’. This process of adjustment depends upon the information flow to the market. With the arrival of new information to the market and attainment of equilibrium, there are two competing hypotheses, namely the mixture of distribution hypothesis (MDH) and the sequential information arrival hypothesis (SIH). The former states that the price change and volume have a joint response to information (Harris, 1986; Touchen & Pitts, 1983) whereas the latter states that information arrives in the market in a sequential random fashion (Copeland, 1976; Jennings et al., 1981). Price volume relation is the main indicator of the structure of that financial market (Karpoff, 1987). Thus by studying the price volume dynamics it would possible to predict the future return with the help of present trading volume. The prime aim of the article is to evaluate empirically the price volume dynamics of the base metal futures market of India. The study uses causality checks which will also explore the different aspects of technical analysis.

Review of Literature

There has been extensive research concerning the price volume dynamics  of different financial assets. Several researchers attempted to identify the contemporaneous relation between return and volume of different asset classes traded at both equity and commodity markets. Researchers have explained it with the help of information flow which not only affects the return but also the trading volume. Gallant et al. (1992) emphasised the joint dynamics of return and trading volume. A change in trading volume indicates the change in investors’ perception because of information flow which affects the price of the asset. Besides other financial assets, the demand and supply model of commodity futures indicates the existence of a strong association between price and trading volume.

According to Biswas and Rajib (2011), ‘a change in demand induces a price change and subsequently adjustment takes place in price and trading volume until a new equilibrium is arrived at’. This process of adjustment depends upon the information flow to the market. With the arrival of new information to the market and attainment, of equilibrium, there are two competing hypotheses, namely the MDH and the SIH. The former states that the price change and volume have a joint response to information (Harris, 1986; Touchen & Pitts, 1983) whereas the latter states that information arrives in the market in a sequential random fashion (Copeland, 1976; Jennings et al., 1981). The MDH proposes that when new information arrives in the market both trading volume and price responds synchronously and information attains equilibrium immediately without any intermediate equilibrium.

According to Biswas and Rajib (2011), the SIH proposes that ‘the information arrives at the market in a sequential random fashion and there are series of intertemporal equilibria before the final complete equilibrium is reached’. It states that because of the sequential flow of information the past values of trading volume are able to predict the future return and vice versa. Thus it implies the existence of causality between the change in trading volume and return.

Several researchers use the Granger causality test for examining the dynamics between the prices and trading volume of a financial asset. Cornell (1981) and Grammatikos and Saunders (1986) examined the currency as well as commodity futures and concluded that there exists a positive correlation between the volume and return. By developing a noise trading model De long et al. (1990) found a positive causal relationship between price and volume. Bessembinder and Seguin (1993) studied both commodity and financial futures markets and supported that unexpected positive volume shocks have a larger effect on volatility than negative volume shocks. Wang (1994) found a positive correlation between trading volume and absolute price change and concluded that information asymmetry increases the association between the two. In their, study Hiemstra and Jones (1994) considered Dow Jones stock return and New York Stock Exchange trading volume and found the existence of unidirectional linear causality from the stock return to trading volume and bidirectional non-linear causality between these two. For examining the existence of non-linear causality they considered Baek and Brock’s (1992) approach. By studying crude oil futures Foster (1995) postulated that the lagged volume of crude oil futures forecasts its absolute value of the return. Fujihara and Mougoue (1997) considered petroleum futures and supported the existence of bidirectional nonlinear causality between the price and volume.

By extending Hiemstra and Jones’s (1994) work Silvapulle and Choi (1999) examined linear and non-linear causality between the stock return and volume traded in the Korean Stock Market and the study exhibits the existence of both bi-directional linear and non-linear causality between the volume and stock return. Moosa and Silvapulle (2000) studied the linear and non-linear causality between the return and trading volume of crude oil futures and confirmed the existence of unidirectional linear causality from trading volume to return and bidirectional non-linear causality between the price and volume. They used a bivariate vector autoregressive (VAR) framework for testing linear causality and considered Baek and Brock’s (1992) approach for testing non-linear causality. Further, they concluded that volume can be used for predicting prices. Ciner (2002) studied the return and trading volume of gold, platinum and rubber futures contracts traded at the Tokyo commodity exchange. The study examined the impact of the information content of volume on price change. He found no linear causality from volume to price change but argued for the existence of bidirectional non-linear causality between change in trading volume and return.

Mcmillan and Speight (2002) investigated the MDH and the SIH by using London Financial Futures and Options Exchange futures data. They examined the dynamic relationship between the trading volume and return by employing the Granger causality test with the VAR framework. The study exhibits causality from the return to trading volume and they argued that there is no apparent causality from the return to volume. Chen et al. (2004) examined the return volume dynamics of the China futures market by using correlation and Granger causality test and found no contemporaneous correlation between return and trading volume but supported the existence of bi-directional causality. Lokman and Abdulnasser (2005) took the stock price and trading volume of different countries, namely the Czech Republic, Russia, Turkey, Hungary and Poland used the linear Granger causality test by following Toda and Yamamoto’s (1995) approach and found no causality between stock price and volume of the Czech Republic. The study reveals unidirectional causality from stock price to volume for Russia and Turkey whereas bidirectional causality is observed for Hungary and Poland.

By considering electricity futures traded at the New York Mercantile Exchange Hadsell (2006) explored the relationship between the trading volume and price and found that the information was slow to be incorporated into the price in two markets and the traders react asymmetrically to the arrival of new information in three markets. Nevin et al. (2006) tested causality using the VAR model proposed by Granger and the nonlinear causality suggested by Peguin-Feissolle and Terasvirta (1999) between the stock price and trading volume of Turkey. The study exhibits unidirectional Granger causality from volume to return. They found strong predictive power of volume. Girard and Biswas (2007) studied 49 equity indices of developed and developing markets and their study supports the MDH. Puri and Philippatos (2008) explored the volume return dynamics of interest rate and currency futures and finds an asymmetric relationship between volume and return.

Biswas and Rajib (2011) considered gold, silver and crude the oil futures of the MCX of India and their study supports the SIH for all three commodity futures. Zwergel and Heiden (2012) studied the German stock market and supported the existence of contemporaneous relation between the return and volume. Srinivasan et al. (2016) studied the Indian stock futures market by taking 25 stock futures contracts and found a positive relationship between return and volume of stock futures. They opined that return volatility influences the trading volume. Darolles et al. (2017) analysed the mixture of distribution hypotheses in the context of liquidity friction and they distinguished liquidity friction into two parts, namely short-term and long-term liquidity frictions. They found the former impact the stock return and affect the traded volume and the latter is responsible for the dynamics of daily return.

By following Mcmillan and Speight (2002), Chen et al. (2004) and Biswas and Rajib (2011) the present study is an attempt to answer the following question. Does the MDH hold for the Indian base metal futures market? Does the market support the SIH? In addition, to explore new insights the study also examines the relationship between return and change in open interest and the relationship between the change of volume and open interest. The next section of the study deals with the data and methodology and the subsequent section discusses the results. The fifth section interprets the results and the last section contains the conclusion of the study.

Data and Methodology

Data

The study is based on the secondary data which is downloaded from the official website of MCX, India for 7 years ranging from 1st April 2013 to 31st March 2020. During this period, the base metal market gained significant momentum and this period is free from any abnormal market fluctuations. The data relating to price, the volume traded and open interest of five base metal futures, namely aluminium, copper, lead, nickel and zinc are downloaded. The study uses the daily log return series of price, log of daily changes in volume and open interest.

Variable Specification

Price: Refers to the log return series of futures price of five base metal futures traded at MCX, India.

Volume: Refers to the log of daily changes in the volume of five base metal futures traded at MCX, India.

Open interest: Refers to the log of daily changes in open interest of five base metal futures traded at MCX, India.

Descriptive Statistics

The basic statistical characteristics of log return series of price, log of daily changes in volume and open interest of five metal futures are analysed by using descriptive statistics such as Mean (X), Standard deviation (v), Skewness (S) and Jarque–Bera statistics. The Jarque–Bera statistics which is employed to test the normality of the series implies that:

 

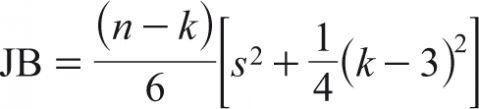         (1)

Where ‘S’ and ‘K’ indicate the coefficient of skewness and kurtosis respectively. ‘n’ refers to the number of observations whereas ‘k’ refers to the number of estimated co-efficient used to create the series.

Unit Root Test

The unit root properties of price, volume and open interest series of different base metals are analysed by performing the Augmented Dickey–Fuller (1979) test as well as the Phillips–Perron (1988) test. The stationarity level of different series of five base metals traded at MCX, India has been checked with the ADF test by fitting a regression equation. The random walk-based regression equation with a drift can be specified as follows:     

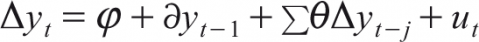      (2)

The hypothesis specified as H₀: = 0, H₁: < 0.

Granger Causality

Causality methodology is developed by Granger (1969) to study whether the change in one series causes another or not. In a set of two series X and Y, if we are able to predict the current values of X, by considering the past values of Y and past values of X including the other relevant information then it is said that Y causes X and vice versa. The above concept of causality is expressed as follows:

    

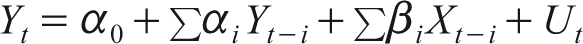     (3)

    ]

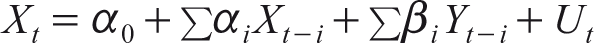      (4)

Where_t indicates time and ‘i’ = 1 to m.

According to Ciner (2002), nonlinear causality from volume to return arises because of the volatility effect. He stated that when lagged volume captures persistence of information flow it will lead to spurious causality. Mcmillan and Speight (2002) studied the contemporaneous relationship between the volume and return and the existence of causality is examined by using the Granger causality test with the VAR framework. Lokman and Abdulnasser (2005) examined causality by using the Granger causality approach with the procedure developed by Toda and Yamamoto (1995). By using OLS regression in the causality test Chen et al. (2004) verified the Granger Causality between the volume and return. They also investigated the contemporaneous relationship between the volume and return by employing Pearson correlation and Spearman rank correlation.

We use both the Augmented Dickey–Fuller (1979) test as well as the  Phillips–Perron (1988) test for testing the unit root properties of the time series. By following Mcmillan and Speight (2002), Chen et al. (2004) and Biswas and Rajib (2011), the Granger causality test is used to examine the causality between the trading volume and return of base metal futures traded at MCX, India. The following VAR framework of causality test is applied only when the data series are stationary.

  

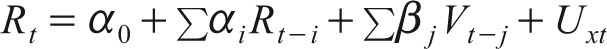   (5)

  

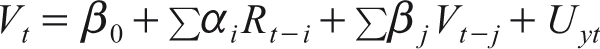    (6)

Where ‘i’ = 1 to m, lag length for the daily return; and ‘j’ = 1 to n, lag length for the daily trading volume.

According to Gujarati (1995), the Granger causality test is sensitive to the number of lags selected for the analysis therefore we have used Akaike information criteria for selecting the lag length of the variable. In the above-specified equations and R indicates return whereas V indicates volume change and both are stationary variables. The null and alternative hypotheses of the above equation can be specified as follows:

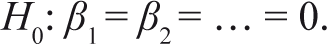
And the alternative hypothesis can be specified as:

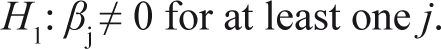
The study will support the MDH if a significant contemporaneous correlation is found between the return and trading volume of different base metal futures. On the other hand, the study will support the SIH if there exists causality between the return and trading volume. Moreover, the study also examines the causality between the trading volume and open interest and between the return and open interest of base metal futures for exploring any newer dimension. For examining the causality between the return and open interest the following equations are specified:

 

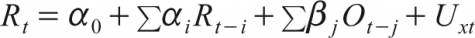                                (7)

 

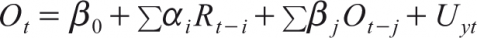                                 (8)

Where ‘i’ = 1 to m, lag length for the daily return; and ‘j’ = 1 to n, lag length for the daily open interest. Similarly for examining the causality between the volume and open interest the following equations are specified:

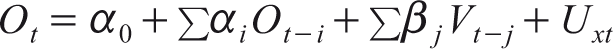                                (9)

 

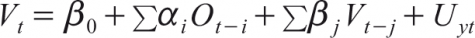                                                           (10)

Where ‘i’ = 1 to m, lag length for the open interest; and ‘j’ = 1 to n, lag length for the daily trading volume.

Empirical Findings

The study considers the daily trading data of all the five base metal futures traded at MCX, India. In order to create a continuous data series volume and open interest, data have been added for all outstanding contracts. The study considers the return series of futures price of five base metal futures, that is, aluminium, copper, lead, nickel and zinc. For this purpose, it is considered that:

 

Where Pt is the daily closing price and Pt–1 is the closing price of the previous day. Similarly, the log of daily changes in volume and open interest of five base metal futures are used for analysis. For this purpose, it is considered that:

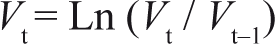
Where Vt is the daily traded volume.

Table 1 indicates basic statistical characteristics of log return series of price, log of daily changes in volume and open interest of five metal futures. The mean daily returns of aluminium, lead and zinc futures are positive whereas it is negative for copper and nickel. The mean log of daily changes in volume and open interest of five base metal futures are negative. Except for copper, the median daily returns of all base metals are zero. The maximum daily return of aluminium, copper, lead, nickel and zinc is 10.25%, 6.14%, 17.72%, 7.26% and 9.36%, respectively. Nickel and aluminium returns register the highest and lowest daily fluctuations respectively.

Table 1. Descriptive Statistics of Return Series

 

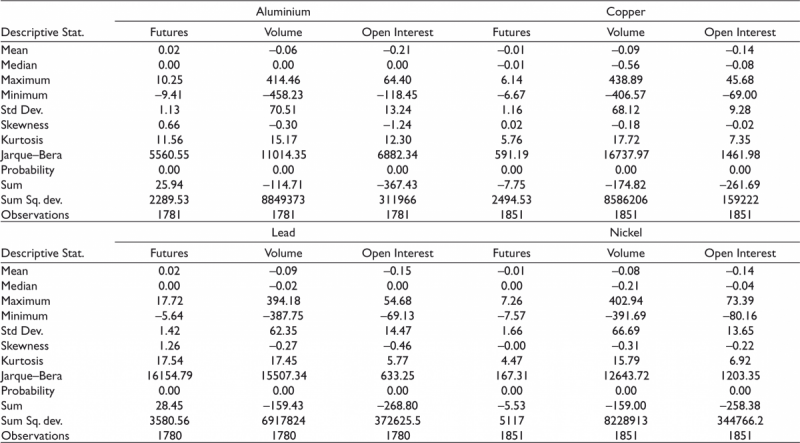
Unlike nickel, all four base metals return series are positively skewed. The daily changes in volume and open interest series of five base metal futures are found to be negatively skewed. The fluctuation in daily changes in the volume of base metal futures is higher than the fluctuation in daily changes in open interest. The fluctuation in daily changes of volume is highest in aluminium whereas it is lowest in the case of lead futures. Similarly, the fluctuation in daily changes of open interest is found to be highest in nickel futures and lowest in copper futures. The kurtosis value is higher than 3 for all daily return series and daily changes in volume and open interest series of all base metal futures, which indicates that all series are leptokurtic, that is, fat tailed. As Jarque–Bera’s p-value is zero for all base metal series hence the null hypothesis of the presence of normality is rejected.

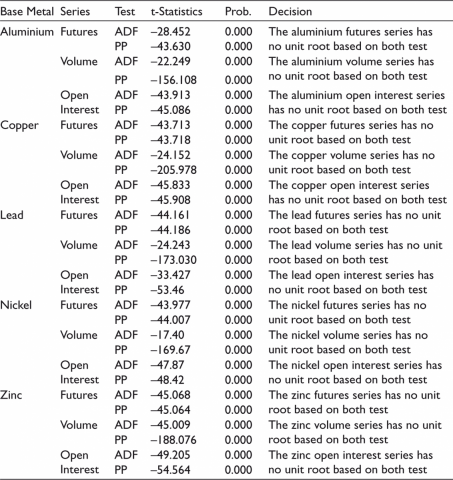
We use the Augmented Dickey–Fuller test (Dickey & Fuller, 1979) and  the Phillips–Perron (1988) (Phillips & Perron, 1988) test for examining the  stationarity of each data series. The results of the stationarity test are tabulated in Table 2. It is evident from Table 2 that all the series of aluminium, copper, lead, nickel and zinc are stationary at level. The p-value of both the stationarity test is zero for all series. As the study uses the Granger causality test to examine the relationship between the various series of different base metal futures hence, the VAR framework of the Granger causality test is applicable to only two stationary series.

Table 2. Unit Root Test

 

The results of both Pearson’s and Spearman’s correlation tests are presented in Table 3. There are three sets of correlation tests have been carried out for each  base metal. The first set of correlations is carried out between the daily return and the daily change of volume. Similarly, the second set of correlations is carried  out between the daily return and the daily change of open interest. We have also explored the correlation between the daily change of open interest and volume. All the coefficients of three sets of correlation of different base metals are found to be significant at a 0.01 per cent level. This is found in both Pearson’s and Spearman’s correlation. Exceptionally it is observed that the Pearson’s correlation coefficient between nickel returns and daily change of volume are not significant at the 0.05 per cent level.

Table 3. Results of Correlation Test

 

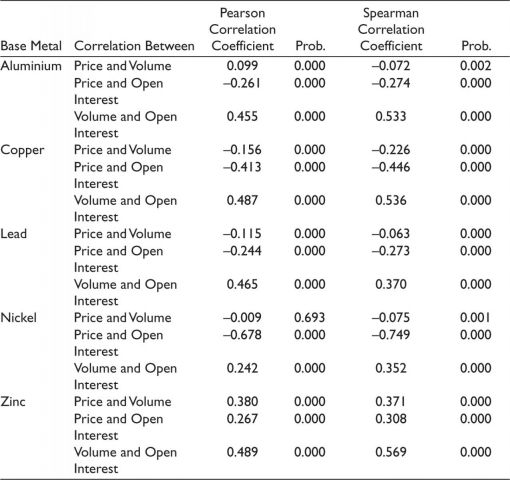
Among all the base metals, the correlation coefficient between return and daily change of volume of zinc is observed to be the highest. It is observed that there exists a contemporaneous correlation between the volume change and return of all base metals. The study also confirms that the correlation between the change in open interest and the return of all base metals is significant. Further, it is also found that a correlation exists between the change in volume and the open interest of all base metal futures.

Granger causality check has three possibilities, namely unidirectional, bidirectional and independent. In a unidirectional situation, one variable influences the other whereas in a bidirectional environment both variables influence each other. No relation is established if it is an independent scenario. As per the Granger causality test, H₀ indicates that one series does not Granger cause the other. If the p-value is less than 0.05 H₀ is rejected and concluded that one series Granger causes the other. Granger causality test results presented in Table 4 exhibit that there is no Granger causality between the volume and return of the base metal futures market of India. The p-values of the Granger causality between volume and return of base metal futures are above 0.05 which depicts an independent scenario. It is further supported by F-statistic values which are also smaller than the critical F-values.

Table 4. Results of Causality Test

 

The study finds unidirectional causality between the return and daily change of open interest. It is found in all base metal futures traded at MCX, India. For aluminium, copper and nickel futures price change, Granger causes the change of open interest. Open interest fails to Granger cause return in all these commodities. On the contrary, causality exists from open interest to return in the case of lead and zinc futures. In the case of aluminium, copper and nickel the study confirms the existence of bidirectional Granger causality between the change in volume and change in open interest. Lead and zinc futures exhibit unidirectional causality from a change in open interest to volume. Interestingly, aluminium, copper and nickel futures show similar behaviour whereas the causality behaviour of lead and nickel futures are different from other base metal futures.

Interpretation of the Results

The study supports the MDH as it confirms the existence of a contemporaneous correlation between the return and change in volume of all base metal futures traded at MCX, India. Coefficient values of zinc futures are highest among other base metals which indicates greater informational asymmetry according to Wang’s (1994) hypothesis. The second set of correlations is carried out between the daily return and the daily change of open interest. We have also explored the correlation between the daily change of open interest and volume. All the coefficients of three sets of correlation of different base metals are found to be significant at a 0.01 per cent level. This is found in both Pearson’s and Spearman’s correlation. The study also confirms that the correlation between the change in open interest and the return of all base metal futures is significant. Further, it is found that a correlation exists between the change in volume and the open interest of all base metal futures. In-depth analysis can be carried out by future studies about the above aspects.

The study exhibits no causality between the return and volume change of aluminium futures which supports the MDH and contradicts the SIH. Similar results are found for all base metal futures. This indicates a greater level of market efficiency (Biswas & Rajib, 2011). As the p-values of F-statistics are greater than 0.05 it rejects the presence of causality between return and volume change of all base metal futures traded at MCX, India.

The study finds unidirectional causality between the return and daily change of open interest. It is found in all base metal futures traded at MCX, India. For aluminium, copper and nickel futures the price change Granger causes the change of open interest. On the contrary, causality exists from open interest to return in the case of lead and zinc futures. In the case of aluminium, copper and nickel the study confirms the existence of bidirectional Granger causality between  the change in volume and change in open interest. Lead and zinc futures exhibit unidirectional causality from the change in open interest to volume. Interestingly, aluminium, copper and nickel futures show similar behaviour whereas the causality behaviour of lead and nickel futures are different from other base metal futures.

Conclusion

After lifting the prohibition on commodity futures trading in India national level commodity exchanges were established (Biswal, 2008). In recent years there has been a spurt in the volume and value of commodity futures trading. The study supports the MDH as it confirms the existence of a contemporaneous correlation between the return and change in volume of all base metal futures traded at MCX, India.

No causality is found between the return and volume change of the base all-metal futures contract which supports the MDH and contradicts the SIH. This indicates a greater level of market efficiency (Biswas & Rajib, 2011). The study finds unidirectional causality between the return and daily change of open interest in all-metal futures. For aluminium, copper and nickel futures the price change Granger causes the change of open interest. On the contrary, causality exists from open interest to return in the case of lead and zinc futures. In the case of aluminium, copper and nickel the study confirms the existence of bidirectional Granger causality between the change in volume and change in open interest. Lead and zinc futures exhibit unidirectional causality from the change in open interest to volume. The relationship between return and daily change of open interest and between change in volume and change in open interest is left for in-depth future study. Further nonlinear causality can also be explored by future research. The study will help the policymakers for framing future policies for developing the market further. It will also help the investors and other participants to make an informed decision.

Declaration of Conflicting Interests

The authors declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.

Funding

The authors received no financial support for the research, authorship and/or publication of this article.

ORCID iD

Laxmidhar Samal  https://orcid.org/0000-0002-4713-6584